A universal speed limit for spreading of coherence
Summary
This Nature paper reports experiments on condensate formation in an isolated, homogeneous Bose gas (39K) confined in a cylindrical optical box. By preparing several far-from-equilibrium initial states and tuning interaction strength via a Feshbach resonance, the authors measure how the coherence length ℓ grows during coarsening. They find robust dynamical scaling with exponent β = 1/2 and a universal coarsening speed D = 3.4(3) ħ/m (≈5.5 μm2 ms−1 for 39K) in the scaling regime. Interaction strength and initial-state differences shift only a non-universal time offset t*, while the long-time growth rate of ℓ2 is independent of n a. The work characterises how the system approaches this speed limit in units set by the healing length ξ and time tξ, and discusses implications across condensed-matter, cosmology and high-energy physics.
Key Points
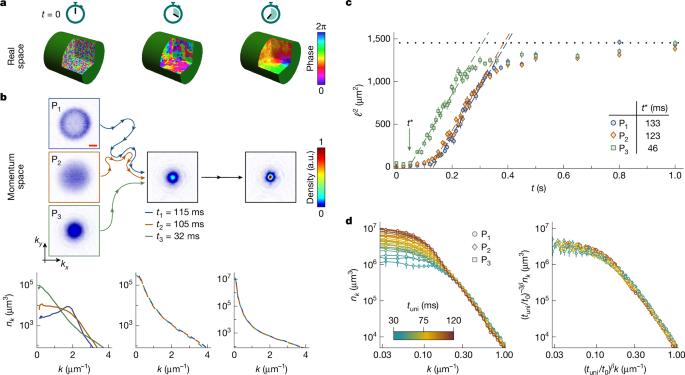
- Experiments on an isolated uniform Bose gas show universal coarsening dynamics quantified by a coherence length ℓ that grows as ℓ ∝ (t − t*)1/2 (β = 1/2) in the scaling regime.
- The measured coarsening speed D ≡ dℓ2/dt = 3.4(3) ħ/m is essentially independent of interaction strength n a and of initial-state details, after accounting for a non-universal time offset t*.
- Initial-state and interaction-strength effects only modify the approach time to the universal regime (t*); weaker interactions require larger ℓ/ξ and larger systems to reach the speed limit.
- Data for different densities, volumes and scattering lengths collapse when expressed in the natural units ξ and tξ, with an approach-to-scaling timescale τ ≈ 56 tξ.
- The result implies a quantum-limited rate for spreading coherence: for macroscopic scales (cm) coarsening by this mechanism would take hours, emphasising practical limits on spontaneous long-range order growth by coarsening alone.
Content summary
The team prepares three distinct far-from-equilibrium momentum distributions (same energy per particle) in a uniform optical box, then turns on interactions and follows relaxation by measuring momentum-space distributions n_k via time-of-flight imaging. After an initial non-universal period, all trajectories enter a scaling regime where low-k n_k collapses to a single universal curve and ℓ2(t) grows linearly with time (implying β = 1/2). By varying scattering length a (50–400 a0), density and box size, they show the linear slope D is unchanged within experimental uncertainty; only t* varies.
The authors interpret the independence of D on n a (for β = 1/2) using dimensional arguments: in Gross–Pitaevskii units the only velocity scale available is set by ħ/m (or the quantum of circulation κ = 2πħ/m). They reconcile finite-system intuition (stronger interactions make condensates appear sooner) by showing interaction strength changes how fast the system reaches the universal regime, not the asymptotic coarsening speed. The data collapse in units of ξ and tξ demonstrates universality across parameters.
Context and relevance
This result tightens our understanding of far-from-equilibrium universality and coarsening in many-body systems. It links nonthermal fixed-point ideas and coarsening kinetics to a concrete, experimentally measured speed limit for the spread of coherence. Because the scaling exponent β = 1/2 and the emergence of a D set by ħ/m appear in theories for both nonrelativistic and ultrarelativistic fields, the findings are relevant far beyond cold atoms: they inform models of early-universe thermalisation, quark–gluon plasma dynamics and quantum turbulence. Practically, the work clarifies when and why interaction tuning speeds up apparent condensation (by reducing t*), and when it cannot beat the universal coarsening speed.
Why should I read this?
Want the short take: they found a reproducible, quantum-set speed limit for how fast phase coherence spreads in a uniform Bose gas. If you care about how order forms in chaotic many-body systems — from lab Bose condensates to analogue-cosmology experiments — this paper tells you when interaction tweaks help and when they don’t. It’s a neat experimental demonstration of theory-grounded universality, and it explains why making coherence over truly large distances is hard.
Author style
Punchy. The paper packs a clear experimental demonstration with tight theory connections — if you’re in many-body physics, ultracold atoms, or interested in universal non-equilibrium dynamics, the details matter and are worth digging into. For others, the main message (a universal D set by ħ/m and β = 1/2) saves you time: you can take this as a robust benchmark for models or simulations.