Aharonov–Bohm interference in even-denominator fractional quantum Hall states
Article meta
Date: 07 January 2026
Source: https://www.nature.com/articles/s41586-025-09891-2
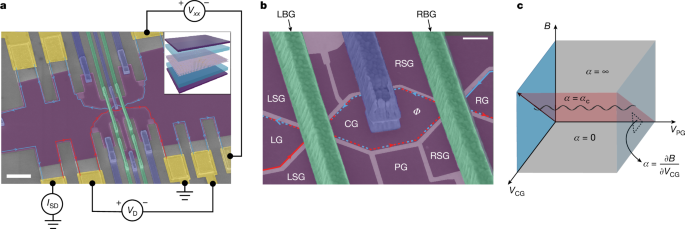
Image: Figure 1 (device)
Summary
This Nature paper reports robust Aharonov–Bohm (AB) interference at two even-denominator fractional quantum Hall (FQH) plateaus in bilayer graphene using a gate-defined Fabry–Pérot interferometer (FPI). The experiments, performed at 10 mK and magnetic fields up to 12 T, reveal an unexpected flux periodicity close to 2 Φ0 when keeping filling constant, implying an effective interfering charge of e* ≈ 1/2 e or, alternatively, double windings of 1/4 e quasiparticles. Complementary measurements at nearby odd-denominator fillings show interfering charges that track the Landau-level filling (e* = νLL e). By moving off the constant-filling trajectories the authors also detect statistical (anyonic) phase contributions consistent with localized bulk quasiparticles of charge 1/4 e. The results mark a significant step towards coherent interferometry of candidate non‑Abelian states in bilayer graphene, while leaving open whether the observed 2 Φ0 periodicity arises from Abelian 1/2 e quasiparticles or non‑Abelian double‑winding of 1/4 e anyons.
Key Points
- Clear AB oscillations observed at two even‑denominator FQH plateaus in bilayer graphene using a gate‑defined Fabry–Pérot interferometer.
- Measured flux periodicity ΔΦ ≈ 2 Φ0 at constant filling, suggesting an interfering charge e* ≈ 1/2 e or double windings of e* = 1/4 e quasiparticles.
- Odd‑denominator states (e.g. ν = 1/3, 2/3) show interference consistent with e* = νLL e rather than the minimal bulk quasiparticle charge in some cases.
- Tuning away from constant filling introduces bulk quasiparticles and reveals a statistical phase contribution consistent with 1/4 e bulk anyons.
- Device: high‑mobility van‑der‑Waals heterostructure with bilayer graphene encapsulated by hBN and graphite gates; lithographic interference area ≈1 μm2; measurements at 10 mK.
- Findings advance two prerequisites for observing non‑Abelian statistics: quasiparticle coherence and contributions from localized bulk quasiparticles, but further tests (e.g. shot‑noise at a single QPC) are needed to distinguish Abelian from non‑Abelian scenarios.
Content summary
The authors fabricated a finely gated Fabry–Pérot interferometer on a bilayer‑graphene vdW stack and measured diagonal resistance oscillations as a function of magnetic field, plunger‑gate voltage and centre‑gate voltage. By following constant‑filling trajectories they isolated the AB contribution and extracted flux periodicities via 2D fast Fourier transforms of the characteristic “pajama” patterns. At ν = −1/2 (hole side) and ν = 3/2 (electron side) they found ΔΦ ≈ 2 Φ0, which maps to an interfering charge of e* ≈ 1/2 e if interpreted via the AB term. The team considered an alternate interpretation where fundamental e* = 1/4 e non‑Abelian quasiparticles execute two windings or where ground‑state fluctuations suppress the 4 Φ0 signal, leaving a robust 2 Φ0 harmonic. Measurements at odd‑denominator and hole‑conjugate states indicate that the interfering charge often follows the partially filled Landau level (e* = νLL e). By deviating from fixed filling they induced bulk quasiparticles and measured slope changes consistent with a statistical phase from localized 1/4 e excitations. Temperature and transmission dependences were explored; visibility drops with temperature but the periodicities remain stable.
Context and relevance
This work sits at the frontier of experimental anyon physics and topological quantum matter. Even‑denominator FQH states (long suspected hosts of non‑Abelian anyons) have been studied in GaAs and graphene, but robust AB interference at such fillings has been elusive. Demonstrating coherent interference and a statistical phase contribution in bilayer graphene brings interferometric probes of non‑Abelian order closer to reality. The finding that the dominant tunnelling charge can be non‑fundamental (e.g. e* = νLL e rather than the smallest bulk quasiparticle) has implications for how QPCs and edge interactions control which excitations participate in transport — crucial for anyon detection and for potential topological qubit schemes.
Why should I read this?
Want the short version — this is the paper that actually gets interference working at even‑denominator states in bilayer graphene, and that’s a big deal if you care about anyons or topological qubits. The experiment shows coherent quasiparticle interference and fingerprints of bulk anyons, but it also leaves a neat puzzle: is the signal from Abelian half‑charge quasiparticles or from non‑Abelian quarter‑charge anyons doing a double loop? If you’re following non‑Abelian detection methods, edge‑mode engineering or interferometer design, this saves you a heap of reading — the authors do the heavy lifting and lay out what to test next.
Author note
Punchy take: the team demonstrates two essential ingredients for interferometric access to non‑Abelian physics — coherence and bulk anyon effects — but the final identification requires targeted follow‑ups (notably shot‑noise at a single QPC and control of QPC tunnelling channels). For experimentalists this paper is a must‑read; theorists will find the tunnelling‑selection puzzles and slope analyses compelling.