Efficient quantum thermal simulation
Summary
The authors present a new, practically motivated quantum algorithm for preparing thermal (Gibbs) states of quantum many-body systems. The core is a synthetic Lindbladian that (i) satisfies exact quantum detailed balance, (ii) remains quasi-local for geometrically local Hamiltonians (radius scaling ~β), and (iii) is implementable with provable resource bounds. The construction replaces exact Bohr-frequency projectors by Gaussian-damped operator Fourier transforms, adds a corrective coherent (Lamb-shift-like) term, and yields an algorithmic Gibbs sampler that mirrors classical MCMC features while avoiding costly high-precision energy measurements.
Key Points
- Exact quantum detailed balance is achieved despite finite energy uncertainty by using Gaussian-smoothed operator Fourier transforms and a shifted KMS condition.
- The proposed Lindbladian is quasi-local: for local Hamiltonians the jump terms act on a ball of radius ~β with exponentially decaying tails (Lieb–Robinson control).
- An explicit coherent term C is prescribed to cancel noncommuting decay contributions and guarantee stationarity of the Gibbs state.
- Implementation uses a phase-estimation-like operator Fourier transform and block-encoded jump operators; Hamiltonian simulation cost scales roughly as Õ(β·t) for time t.
- The authors provide almost linear-time Lindbladian simulation algorithms (diamond-norm guarantees) and resource estimates for block encodings and ancilla use.
- Mixing behaviour depends on model and choice of jumps; numerical diagonalisation on small spin chains shows fast gaps at high temperature and problem-specific slowdowns at low temperature that can be mitigated by global or multi-site jumps.
Content summary
Classical MCMC (Metropolis, Glauber) relies on detailed balance and locality to sample thermal distributions efficiently. Quantum analogues have struggled: earlier quantum Metropolis proposals are nonlocal, break detailed balance, or rely on hard-to-verify assumptions. The paper constructs a Lindbladian that is both algorithmically implementable and satisfies quantum (KMS) detailed balance exactly.
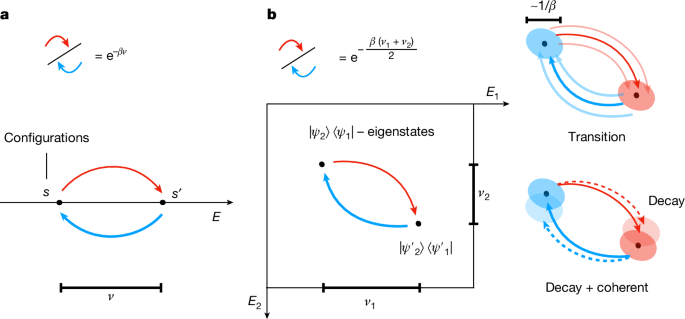
The technical innovation is to replace exact Bohr-frequency projectors A_ν by a Gaussian-weighted operator Fourier transform Â(ω), which retains adjoint and conjugation symmetries needed for detailed balance while only requiring energy resolution ~1/β. The transition weights γ(ω) are shifted to satisfy a modified KMS relation, and a coherent term C is added to ensure the decay part does not break balance when it fails to commute with H.
The authors provide circuit-level constructions: a discretised operator Fourier transform (phase-estimation style), a first-order weak-measurement circuit to implement small time steps of the Lindbladian, and compression/bootstrapping techniques to approach almost linear-in-time complexity with polylog accuracy overhead. Theorem statements give resource bounds and locality/uniqueness conditions for the Gibbs fixed point.
Context and relevance
This work plugs a major conceptual gap: a principled, efficient quantum analogue of classical MCMC that respects quantum detailed balance. That matters because preparing thermal states is central to materials simulation, condensed-matter physics, quantum chemistry and machine-learning-inspired sampling tasks. The algorithm is especially relevant to the forthcoming fault-tolerant era: it gives a clear roadmap, with provable costs, for Gibbs-state preparation on large quantum devices and for further theoretical study of mixing times and phase-dependent slowdowns.
Beyond physics, MCMC underpins many applied fields; a reliable quantum MCMC could become a foundational quantum subroutine across optimisation, Bayesian inference and probabilistic modelling, provided mixing is favourable for problems of interest.
Why should I read this?
Short version: if you care about preparing thermal states on a quantum computer (or about whether quantum machines can beat classical methods for low-temperature many-body problems), this paper is essential. It gives a concrete algorithm, proofs, resource estimates and small-system numerics — so you don’t have to wade through half-baked proposals. If you just want the takeaway: they’ve found a physically inspired, implementable route to quantum Gibbs sampling that keeps locality and exact detailed balance while avoiding costly precision in energy measurement.