Surface optimization governs the local design of physical networks
Article meta
Article Date: 07 January 2026
Article URL: https://www.nature.com/articles/s41586-025-09784-4
Article Image: Figure 1
Summary
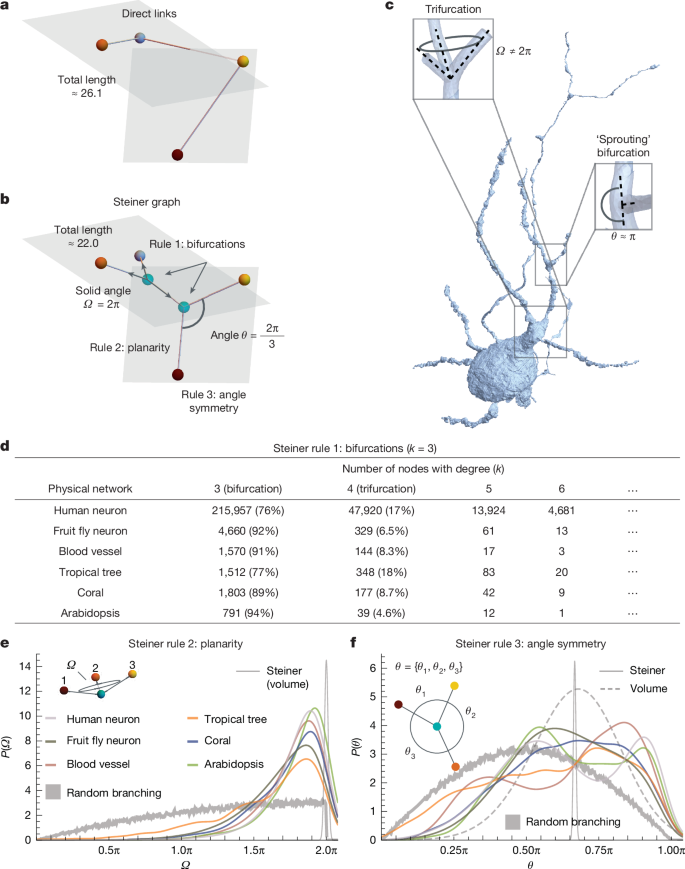
This Nature paper argues that many real-world physical networks (neurons, blood vessels, trees, corals, plant roots) are better described by surface-area minimisation of smooth two-dimensional sleeve-like charts sewn over links, rather than by classical one-dimensional wiring (length) or simple cylindrical volume minimisation. Using recent high-resolution 3D reconstructions from six classes of networks, the authors document systematic deviations from the Steiner/length-minimisation predictions: higher-degree nodes (trifurcations and above), non-planar junctions and broadly distributed branch angles.
To explain these departures they recast the local network motif as a surface minimisation problem on a manifold associated with the graph and show a formal mapping to higher-dimensional Feynman-diagram (string-theory) worldsheets. That mapping lets them compute minimal surfaces numerically (code: min-surf-netw) and derive testable predictions: a thickness-dependent transition from bifurcations to stable trifurcations, and a regime of orthogonal “sprouting” when one branch is much thinner. They validate these predictions across the six datasets and provide dataset and code links.
Key Points
- Classical optimal wiring (Steiner) treats links as 1D wires; volume-based approaches treat links as simple cylinders—both miss surface-driven constraints of real 3D links.
- Empirical data (human and Drosophila neurons, human vasculature, tropical trees, corals, Arabidopsis) show consistent violations of Steiner predictions: ~15% or more nodes with degree k>3, non-planar junctions and broad angle distributions.
- Authors formalise physical networks as 2D manifolds (sleeves) over graph links and replace total length with total surface area subject to minimum circumference constraints (w), yielding a surface-minimisation optimisation.
- They find a formal equivalence between the surface problem and string-theory worldsheets (Feynman-diagram generalisation), enabling analytic and numerical treatment via the min-surf-netw package.
- Surface minimisation predicts a thickness parameter (χ = w/r) driven transition: for χ ≈ 0.83 the system moves from paired bifurcations (Steiner-like) to a single stable trifurcation (k = 4), explaining observed trifurcations.
- Angle asymmetry: when one branch is thinner (ratio ρ below a threshold) the model predicts orthogonal sprouting (perpendicular small branch) — a widespread motif found empirically and frequently used functionally (e.g. neuronal synapses).
- Model reproduces conditional angle distributions and provides falsifiable fingerprints (P(λ), P(Ω)) that match measurements across datasets.
- Data and code are public: dataset at https://physical.network and code at https://github.com/Barabasi-Lab/min-surf-netw.
Context and relevance
This work reframes the design principles of material networks by emphasising surface and local geometry rather than just length or simple volume. That shift matters for fields that design or interpret branching structures — neuroscience (dendritic/spine formation), vascular biology, plant root architecture, tissue engineering and biomimetic network design. It offers a principled explanation for previously puzzling motifs (trifurcations, orthogonal sprouts) and supplies tools and datasets to test ideas further.
Author style
Punchy: this is a significant conceptual advance — not just another numerics paper. The authors link empirical 3D data to a fresh optimisation principle and a surprising bridge to string-theory tools. If you work on physical, biological or engineered branching systems, the methods and falsifiable predictions here are worth digging into.
Why should I read this
Short version, no fuss: if you’ve ever wondered why real branches don’t match textbook “shortest-wire” trees, this paper explains it. Real links have width and surface, they sew together smoothly, and that surface cost changes local design — giving trifurcations and perpendicular sprouts you actually see in data. It’s clever, surprisingly practical and comes with data + code.